Geany 配置 Python
本文共 222 字,大约阅读时间需要 1 分钟。
我的电脑里有两个 Python,一个是平常的 Python,是在 Python 官网上下载的;另一个是在 MiniConda 上带来的。
平时用的是平常的 Python,但有一天想改成 miniconda 的 python,此时就要修改一下了:
首先: Build -> Set Build Conmmands
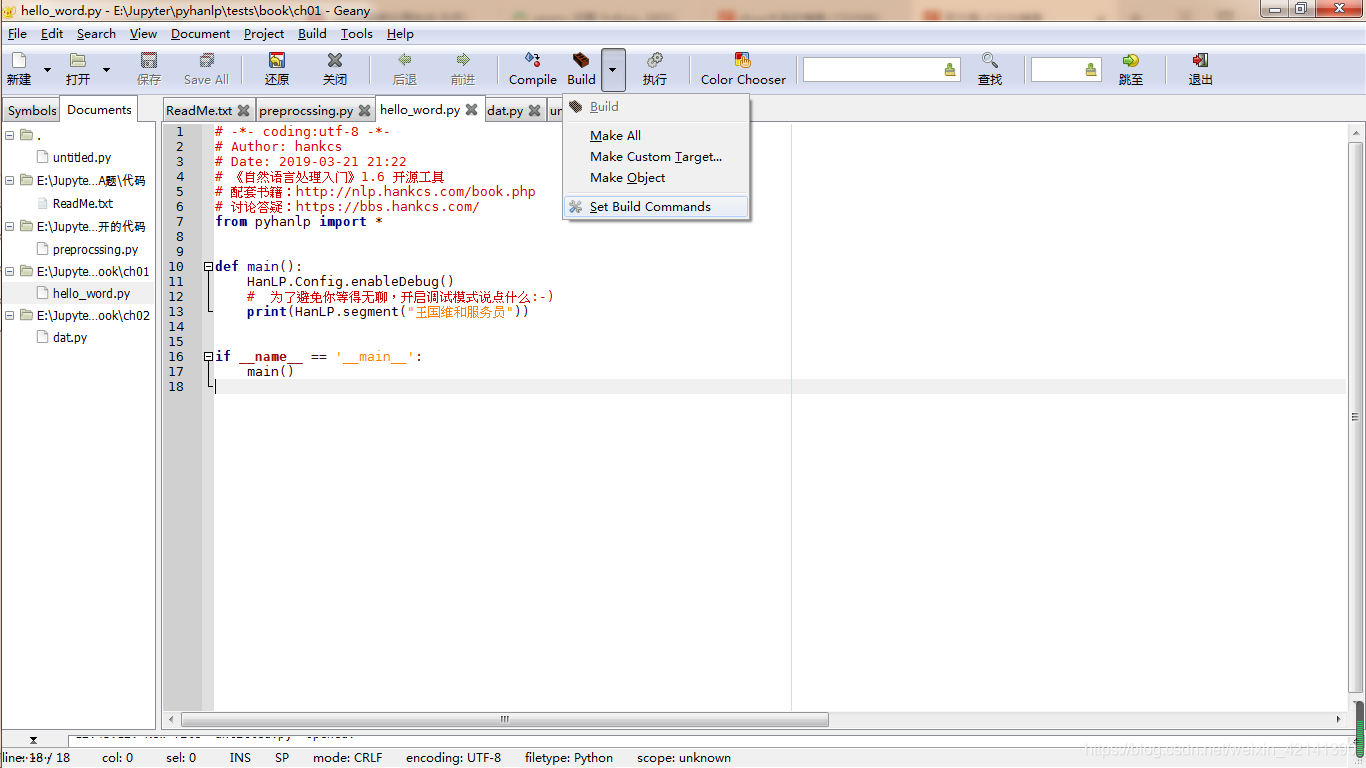
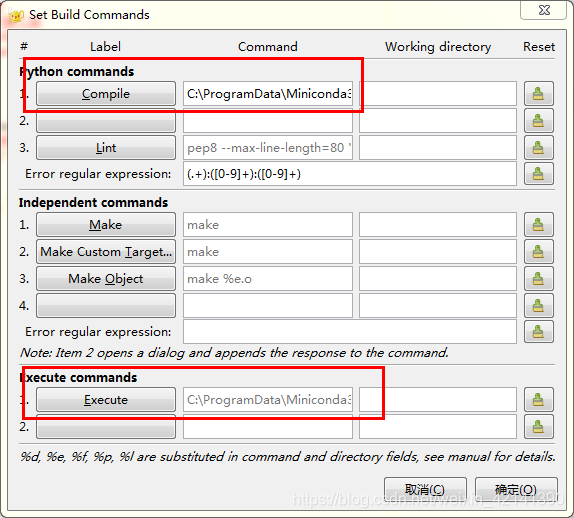
然后修改 Compile 和 Execute,将 -m 前和 “%f” 前 的 py 改成你想配置的 Python.exe 的路径:
转载地址:http://eqsg.baihongyu.com/
你可能感兴趣的文章